(本文图片引用自 Amit Patel 的博客)
在游戏中,我们常常会遇到寻找两点之间最短路径的任务。而寻路算法中比较经典的就是 *A 算法** 了。实际上,对于理解了它的人来说这是个很简单的算法,但对于不了解的人来说,可能这是一个比较复杂的算法。
理解一个复杂概念的最好办法便是由浅入深,A* 算法的提出也并非一蹴而就,它也是由一些简单的算法改造而来的。本文尝试带你一步步去学习 A* 算法的基本知识,帮助你理解这个算法。
最简单的寻路——贪心算法
一个最简单的寻路算法便是直接计算起点各个方向到终点的距离,选择最小的那个方向走一步就可以了。这个算法理解起来很直观,计算量也不大,某些情况下是很好的算法,比如下图所示:

然而,这个算法有一个缺点:过于“短视”,只考虑了一步,如果途中有障碍物,必须等到撞上了障碍物才回头走另外的路,这时候找到的路径也不是最短的,就像下面的情况:
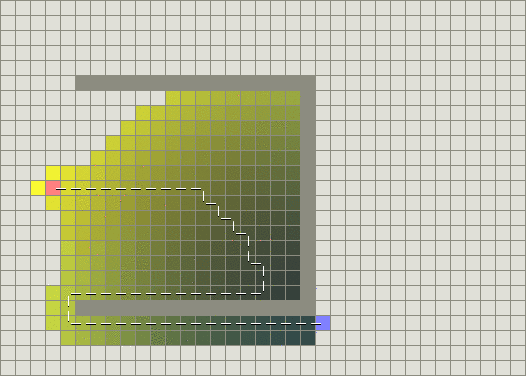
一定正确的寻路——Dijkstra 算法
为了解决贪心算法的缺点,Dijkstra 算法则采用了一种更加“目光长远”的搜索方式,它不仅仅只看当前方向可以走的下一步,还会在下一步的基础上再进一步搜索下去,直到找到一条到终点的路径为止。
Dijkstra 算法事实上有点像带了记忆的 BFS 算法(深度优先搜索),它采用了一个队列记忆即将要搜索的节点,还有一个数组来记录各个节点到起点的最短距离,如果队列不空的话就从里面取出一个进行扩展,并更新距离数组,循环直到到达终点或者队列已经清空的情况则终止搜索。关于 Dijkstra 的详细算法,本文不再赘述,可以到网上搜索相关文章学习。
Dijkstra 算法保证找到的路径是最短的,不会出现绕远路的现象:

但是相比于贪心算法,它也有一个缺点:搜索量太大了,贪心算法很快就能找到的路径,Dijkstra 算法很可能要搜索多不少的节点:

有没有搜索又快又准的算法呢?有!那就是大名鼎鼎的 A* 算法了!
又快又准的寻路——A* 算法
启发式搜索
观察 Dijkstra 算法和贪心算法的尝试节点,我们会发现 Dijkstra 在搜索时会搜索一些明显很差的节点,如果我们能用某种办法来衡量一个节点是否应该被搜索,就可以一定程度上减少 Dijkstra 的搜索量,加快算法速度。那么这个办法是什么呢?那就是在 Dijkstra 算法基础上加上一个启发式搜索的思想,也是 A* 算法最重要的思想。
我们先来看一个简单的公式:$ f(n)=g(n)+h(n) $
如果你在别的地方想学习 A* 算法,一定也会看见这条公式。这条公式为启发式搜索提供了判断依据,其中f(n)表示一个节点的“搜索代价”,越小越好;而f(n)有两个计算依据:一个是g(n),是当前节点到起点的真实距离;另一个是h(n),是当前节点到终点的“估算距离”。g(n)的计算方法很简单,就是前一个节点的g(n)值加上两节点之间的距离,而h(n)则不能随便选取,需要满足启发一致性,也就是 h(n) <= c(n, n’) + h(n’),其中 n’ 是 n 的所有邻接节点,c 是两个节点间的真实距离,并且要满足 h(G) = 0,其中 G 是终点,如果可以上下左右四个方向移动,一般采用的是曼哈顿距离,如果可以朝八个方向移动,则一般采用欧几里得距离。
这条公式有两种特殊情况:
1、h(n)=0,意味着算法没有任何的启发性,退化为效率较低的 Dijkstra 算法。
2、g(n)=0,意味着算法没有任何的准确性,退化为未必最短的贪心算法。
而 A* 算法搜索时,不再一一扩展搜索队列中的每一个元素,而是只扩展搜索队列中f(n)值最小的那一个节点,这样就可以避免少搜索很多的节点。
话不多说,来看看代码:
// map 数组记录了地图,也就是某个节点可不可以走
// visited 记录了某个节点是否被访问过了
// to_visit 记录某个节点是不是在搜索队列中
// open 搜索队列
// 将起点加入到搜索队列中
start.h_value = start.f_value = h_dist(start, end);
start.g_value = 0;
open.add(start);
while (!open.empty()) {
shared_ptr<Node> cur(new Node);
// 获取 f 函数最小的一个节点
*cur = open.getMin();
visited[cur->y][cur->x] = true;
to_visit[cur->y][cur->x] = false;
// 到达了终点
if (*cur == end) {
printPath(cur)
break;
}
for (int i = 0; i < 4; ++i) {
int ny = cur->y + dy[i], nx = cur->x + dx[i];
// 确保数组不越界
if (ny <= max_y && ny >= 0 && nx <= max_x && nx >= 0)
if (!visited[ny][nx] && map[ny][nx] != BLOCK) {
// 计算新的 g 函数值,右边的 + 1 可以依照需要替换为两个节点的距离
int tmp_g_value = cur->g_value + 1;
bool better = true;
Node next;
next.y = ny;
next.x = nx;
if (to_visit[ny][nx]) {
next = open.find(next);
}
// 如果之前记录的 g 值比新的小,说明新的绕了远路,放弃更新
if (next.g_value < tmp_g_value)
better = false;
if (better) {
// 用于构造最短路径
next.parent = shared_ptr<Node>(cur);
next.g_value = tmp_g_value;
next.h_value = h_dist(next, end);
next.f_value = next.g_value + next.h_value;
if (!to_visit[ny][nx]) {
open.add(next);
to_visit[ny][nx] = true;
}
}
}
}
}相信上面的代码可以给你一定的启发,编写自己的 A* 算法。
更多的优化
在上面的算法中,如果我们使用遍历搜索队列的办法来找到f(n)最小的函数,那么算法复杂度达到O(n^2)。这一部分可以采用优先队列或者小根堆的办法来实现O(n\log n)的算法复杂度。
希望本文可以帮助你理解 A* 算法。其实许多的算法也是从简单的情况入手,慢慢寻找条件优化时间的,我们学习比较复杂的算法的时候也可以用这样的方法来帮助自己学习。