对率几率回归(Logistic Regression)是机器学习中一种基本的分类算法,可以用来完成对输入数据的二分类任务。本文记录了使用 numpy 从基础的公式出发,逐步实现 Logistic Regression 的过程。
目录
对数概率几率函数
我们很容易想到二分类方法可以用阶跃函数(Step Function)来分类,但是阶跃函数不连续、不可导,无法训练,因此我们可以用 S 型函数(Sigmoid Function)来进行预测。
\sigma (x) = \frac{1}{1 + e^{-x}}
$$

Sigmoid 函数及其图像
该函数实际上是一种概率分布函数,它表示的是随机事件发生的概率 $P(X\leq x)$。该函数有着单调递增,连续以及值域在 $[0, 1]$ 等良好特性,常常被用于机器学习的任务中。
而它有一个有趣的性质,它的导数也可以用它本身来表达,即
\sigma'(x) = \sigma(x)(1-\sigma(x)) \tag{*}
$$
推导过程如下:
\frac{\mathrm{d}}{\mathrm{d}x}\left( \frac{1}{\sigma(x)}\right) = -\frac{\sigma'(x)}{\sigma ^2 (x)} \tag{1}
$$
\frac{\mathrm{d}}{\mathrm{d}x}\left( \frac{1}{\sigma(x)}\right) = -e^{-x} = -\frac{1}{\sigma(x)}+1 \tag{2}
$$
两式联立就得到了 $(*)$ 式。
假设数据的两个分类服从伯努利分布,则有 $P(样本是正例)=\phi$,$P(样本是负例)=1 – \phi$。我们的目标就是要找到一个映射函数 $f:R^{n+1}\rightarrow R$,将样本的特征映射到一个实数上,然后再根据函数值进行分类。
假设样本向量为 $\vec x$,可以得到分类公式:
P(Y = 1|{\bf x}) = p = \frac{1}{1 + e^{-\bf W x}}
$$
P(Y = 0|{\bf x}) = 1 – p = \frac{e^{-\bf Wx}}{1 + e^{-\bf W x}}
$$
两式相比并取对数,得到:
\ln\frac{p}{1-p} = \bf W x
$$
式子的意义是样本是正例的概率与样本是反例的概率的比值的对数等于 $\bf W x$,这就是对数概率回归的名字由来。对率回归就是要找到合适的参数 $\bf W $,也就是找到样本空间伯努利分布中的 $\phi$。
参数学习
对于一些给定的样本,我们可以采用极大似然估计法来估计最佳的模型参数。假设我们有 $m$ 个样本,输入特征有 $n$ 个,那么设 $P(Y = 1|\vec x)=\phi(\vec x)$,$P(Y = 0|\vec x)=1-\phi(\vec x)$,得到似然估计函数为:
\prod_{i=1}^{m}[\phi(\vec {\bf x_i})]^{y_i}[1-\phi(\vec {\bf x_i})]^{1-y_i}
$$
将其取对数得到:
L({\bf W}) = \sum_{i=1}^{m}{y_i}\ln\phi( {\bf x_i}) + (1-y_i)\ln(1-\phi( {\bf x_i}))
$$
最大化$L({\bf W})$,即最小化$J({\bf W}) = -L({\bf W})$。
通常使用梯度下降法和拟牛顿法来求最佳参数,本文两种方法都实现了。
代码实现
以下代码规定 ${\bf W}$ 为 $n+1$ 维行向量, ${\bf X}$ 为 $(n + 1) \times m$ 维的输入样本矩阵,${\bf y}$ 为 $m$ 维行向量,为输入数据对应的类别。
sigmoid 函数
按照定义,我们可以定义 sigmoid 函数如下:
def sigmoid(X):
return 1 / (1 + np.exp(-X))但是在实际应用中,指数函数很有可能发生溢出问题,所以使用下面这个函数来代替计算 sigmoid 函数。
def sigmoid(X):
# More stable
return .5 * (1 + np.tanh(.5 * X))Loss 函数
上文中的 $J({\bf W})$ 可以理解为分错类的分数,最小化这个函数就相当于使得模型尽可能少错分类。同样按照公式直接写出 loss 函数,对$J({\bf W})$除以$m$可以使得梯度较小。不同的是这里加入了正则化项,以避免过拟合的问题。同时,为了避免对数函数的输入为 0, 对输入要加上一个小的正数 $\epsilon=10^{-8}$。
为了效率起见,使用了向量化技巧。
def loss(X, y, parameters, lambd):
m = X.shape[1]
g = sigmoid(np.dot(parameters, X))
# Aviod divided by zeros
epsilon = 1e-8
J = -(np.dot(np.log(g + epsilon), y.T) + np.dot(np.log(1 - g + epsilon), (1 - y).T)) / m
J += lambd / (2 * m) * np.linalg.norm(parameters[0, 1:]) ** 2
return J梯度函数
对 $J({\bf W})$ 求导,直接将数据代入公式即可。
def gradients(X, y, parameters, lambd):
m = X.shape[1]
gradients = np.dot((sigmoid(np.dot(parameters, X)) - y), X.T) / m
gradients += np.hstack((0, lambd / m * gradients[0, 1:]))
return gradients梯度下降法
更新公式为:${\bf W} := {\bf W} – \alpha \nabla J({\bf W})$,其中 $\alpha$ 为学习率。学习率的选取至关重要,会影响模型的训练效果。过大可能导致 Overshooting,错过最优解并朝着反方向前进,过小会导致学习过慢。
class GradientDescentOptimizer(Optimizer):
def __init__(self, X, y, parameters, loss_function, gradients_function, learning_rate = 0.001, lambd = 0.01):
Optimizer.__init__(self, X, y, parameters, loss_function, gradients_function)
self.learning_rate = learning_rate
self.lambd = lambd
def step(self):
gradients = self.gradients(self.X, self.y, parameters=self.parameters, lambd=self.lambd)
self.parameters -= self.learning_rate * gradients
loss = self.loss(self.X, self.y, parameters=self.parameters, lambd=self.lambd)[0][0]
return loss在实验中,发现对于给定的测试数据,学习率的选取必须非常小,否则极其容易训练失败,而学习率的选取并不容易,为了避免手动选取学习率的麻烦,我们可以采用牛顿法。
牛顿法
要找到函数的极小值点,我们可以通过解方程 $\nabla J({\bf W})=0$ 来得到估计的参数值。一般情况下这个方程难以直接求解,但是可以通过牛顿法迭代来找到方程的解。牛顿法的一维情形是:
x_{n+1} = x_{n} – \frac{f(x_n)}{f'(x_n)}
$$
从泰勒展开的理解便是函数在 $x_n$ 处的泰勒式等于零来近似求解方程:
f(x) = f(x_n) + f'(x_n)(x – x_n) + o(x_n)
$$
若果要求 $f'(x)=0$ 的解,直接替换上式中的 $f(x)$,$f'(x)$ 为 $f'(x), f”(x)$ `即可。对于高维情形则是:
x_{n+1} = x_{n} – [{{\bf H}f(x_n)}]^{-1}{\nabla f(x_n)}
$$
其中 $[{{\bf H}f(x_n)}]^{-1}$ 为黑塞矩阵的逆矩阵,黑塞矩阵是函数的二阶偏导数排列而成的矩阵。
阻尼牛顿法
牛顿法有一个缺点:某些时候更新后的参数并不能稳定地收敛到零点,严重的情况下会导致点列 $\{x_n\}$ 发散而迭代失败。为了改进这一缺点,在对参数更新之前,先进行一维搜索,找到使函数下降最快的一个方向,然后再对参数进行更新。这种方法也叫 Line Search,即找到一个参数 $\alpha^* = \arg \min_{\alpha \in \bf{R}} f(x_n – \alpha[{{\bf H}f(x_n)}]^{-1}{\nabla f(x_n)})$,然后再根据找到的方向进行参数更新。 Line Search 方法比较冗长,具体请参考代码。在此不再贴出。
class NewtonMethodOptimizer():
def __init__(self, X, y, parameters, loss_function, gradients_function, second_derivatives_function, lambd=0.01, epsilon=1e-6):
Optimizer.__init__(self, X, y, parameters, loss_function, gradients_function)
self.second_derivatives = second_derivatives_function
self.lambd = lambd
self.epsilon = epsilon
def step(self):
n, m = self.X.shape
gradients = self.gradients(self.X, self.y, parameters=self.parameters, lambd=self.lambd)
H = self.second_derivatives(self.X, self.y, parameters=self.parameters, lambd=self.lambd)
d_k = -np.dot(gradients, np.linalg.pinv(H))
f = lambda alpha : self.loss(self.X, self.y, parameters=self.parameters + alpha * d_k, lambd=self.lambd)
alpha = line_search(self.X, self.y, f)
self.parameters += alpha * d_k
loss = self.loss(self.X, self.y, parameters=self.parameters, lambd=self.lambd)[0][0]
return loss拟牛顿法
由于牛顿法需要用到函数的二阶导数,计算较为不便,而且需要求解黑塞矩阵的逆,时间复杂度高,为此人们提出了通过迭代来近似黑塞矩阵的拟牛顿法,其中较为知名的有 DFP 算法和 BFGS 算法,本文实现了 BFGS 算法。
BFGS 的原理如下,由泰勒公式我们有
\nabla J({\bf W}) = {\nabla J({\bf W_{k+1}}) + {\bf H}J({\bf W_{k+1}})({\bf W} – {\bf W_{k+1}}) }
$$
代入${\bf W} = {\bf W_{k}}$,并记 $[{\bf H}J({\bf W_{k+1}})]^{-1} = {\bf D_{k+1}}$,${\bf W_{k+1}} – {\bf W_{k}}={\bf s_k}$,$\nabla J({\bf W_{k+1}})-{\nabla J({\bf W_{k}})} = {\bf y_k}$, 得到:
{\bf s_k} = {\bf D_{k+1}}{\bf y_k}
$$
根据牛顿法迭代公式,并应用 Line Search 方法,又有 ${\bf s_k = -\alpha^*D_kg_k}$
记黑塞矩阵的近似矩阵为${\bf B_k}$,则有
{{\bf B_{k+1}}={\bf B_k} + \alpha {\bf uu}^{\sf T}+\beta {\bf vv^{\sf T}}}
$$
{\bf B_{k+1} s_k=y_k}={\bf B_k s_k} + \alpha {\bf uu}^{\sf T}{\bf s_k}+\beta {\bf vv^{\sf T}}{\bf s_k}
$$
通过令${\bf u = y_k}$,${\bf v=B_k s_k}$,可以得到:
{{\bf B_{k+1}}={\bf B_k} + \frac{\bf y_ky_k^\sf T}{\bf y_k^{\sf T}s_k} – \frac{\bf B_ks_ks_k^{\sf T}B_k}{\bf s_k^{\sf T}B_ks_k}}
$$
对其应用 Sherman-Morrison 公式求逆得到(这里我不太会推导,是参考书上的):
{\bf D_{k+1}=\left(\bf I – \frac{s_ky_k^{\sf T}}{y_k^{\sf T}s_k} \right)D_k\left(I-\frac{s_ky_k^{\sf T}}{y_k^{\sf T}s_k}\right)^{\sf T} + \frac{s_k s_k^{\sf T}}{y_k^{\sf T}s_k}}
$$
只要初始矩阵 ${\bf D_0}$ 是正定的,那么 ${\bf D_k}$ 就是正定的,所以我们可以选择 ${\bf D_0 = I}$
至此我们就完成了黑塞矩阵逆矩阵的更新,参考代码如下:
class BFGSOptimizer(Optimizer):
def __init__(self, X, y, parameters, loss_function, gradients_function, lambd=0.01, epsilon=1e-6):
Optimizer.__init__(self, X, y, parameters, loss_function, gradients_function)
self.lambd = lambd
self.epsilon = epsilon
n, m = X.shape
self.D_k = np.eye(n)
self.g_k = self.gradients(self.X, self.y, parameters=self.parameters, lambd=self.lambd)
self.s_k = np.zeros((1, n))
self.d_k = np.zeros((1, n))
self.y_k = np.zeros((1, n))
def step(self):
n, m = self.X.shape
self.d_k = -np.dot(self.g_k, self.D_k)
f = lambda alpha : self.loss(self.X, self.y, parameters=self.parameters + alpha * self.d_k, lambd=self.lambd)
alpha = line_search(self.X, self.y, f)
self.s_k = alpha * self.d_k
self.parameters += self.s_k
old_g = self.g_k.copy()
self.g_k = self.gradients(self.X, self.y, parameters=self.parameters, lambd=self.lambd)
self.y_k = self.g_k - old_g
# Update inversed approximate Hessian matrix
ys = np.dot(self.y_k, self.s_k.T)
ident = np.eye(n)
mat_left = np.asmatrix((ident - np.dot(self.s_k.T, self.y_k) / ys))
mat_right = np.asmatrix(mat_left.T)
self.D_k = mat_left * np.asmatrix(self.D_k) * mat_right + np.dot(self.s_k.T, self.s_k) / ys
loss = self.loss(self.X, self.y, parameters=self.parameters, lambd=self.lambd)[0][0]
return loss
BFGS 虽然需要迭代的次数较牛顿法更多,但却避免了二阶导数的计算,也没有矩阵的直接求逆,提升了运行效率。
运行效果
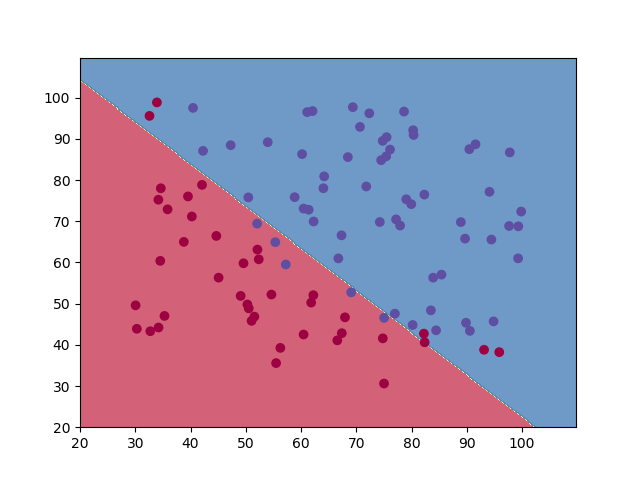

完整代码
完整代码请参考:logistic_regression.py,数据来自 Andrew Ng 的 Machine Learning Coursera 课程,如有任何建议和想法欢迎交流!
注:通常 BFGS 存储完整的 ${\bf D_k}$ 较为消耗内存,尤其是当特征维数很大的时候,可能会占用几十 GB 的内存,这是普通计算机很难承受的,为此人们也提出了 L-BFGS 算法,目前本文还没有实现,也为了避免文章过于冗长,选择在另一篇博文继续更新。