二叉搜索树
二叉搜索树(Binary Search Tree)是一种简单经典的数据结构,其特点有三:
- 一个结点的左子树的值都比该结点的值要小
- 一个结点的右子树的值都比该节点的值要大
- 没有两个结点拥有相同的值
得益于二叉树的特性,支持在 O(\lg n) 的时间复杂度内进行查询操作。本文将介绍一个二叉搜索树的建立、查询以及删除节点操作。
结点的表示
二叉搜索树也是二叉树,结点的表示和普通的二叉树没有什么区别。最简单的情况下,有一个存放数据的数据域,以及指向左右子树的指针。
template<class T>
struct TreeNode {
T data;
TreeNode<T> *pLeft, *pRight;
};二叉搜索树类
为了代码的条理性,首先定义一个 BST 类,存放根节点指针,并提供一系列操作树的方法。
template<class T>
class BST {
public:
BST();
// 用于查找结点
TreeNode<T> *find(T key);
// 用于插入结点
TreeNode<T> *insert(T data);
// 用于删除结点
TreeNode<T> *remove(T key);
// 中序遍历二叉搜索树
void mid_traverse(void (*f)(TreeNode<T> *node));
~BST();
private:
// 由于二叉树具有分形结构,对其进行遍历操作时用递归函数比较方便,特建立以下的辅助函数
static void destroy_tree(TreeNode<T> *root);
static void do_mid_traverse(TreeNode<T> *root, void (*f)(TreeNode<T> *node));
// 存放树的根结点
TreeNode<T> *root;
};二叉搜索树的结点插入
如果一个二叉搜索树的根结点为空,那么直接让该结点成为根结点即可;否则,递归执行以下过程:比较要插入的值与当前树的根的值的大小,如果更小,则让根的左结点成为新的根;如果更大,则让根的右结点成为新的根,直到根为空。
可以看出,以上过程没有区分一个当前的根处于原来的二叉搜索树中的什么位置,也不用管一个结点的左右指针是否为空,只要不停迭代,直到根为空,就将新的值插入即可。
由于我们简化了判断过程,直接修改结点的左右指针,所以我们需要用到二重指针来完成插入操作,具体见代码:
template<class T>
TreeNode<T> *BST<T>::insert(T data) {
TreeNode<T> *pNode = new TreeNode<T>{data, nullptr, nullptr};
TreeNode<T> **curRoot = &root;
while (*curRoot) {
if (data == (*curRoot)->data) return *curRoot;
if (data < (*curRoot)->data) {
curRoot = &((*curRoot)->pLeft);
} else {
curRoot = &((*curRoot)->pRight);
}
}
*curRoot = pNode;
return pNode;
}二叉搜索树的结点查找
二叉搜索树的查找比插入还简单一些,同样是递归操作,按照二叉搜索树的特性,如果当前根结点的值恰好就是要找的值,那么直接返回即可;如果要找的值比根结点要小,就让左结点变为新的根,否则就让右结点变为新的根。
这里并不涉及到左右指针的修改问题,所以直接用一重指针即可。
template<class T>
TreeNode<T> *BST<T>::find(T data) {
TreeNode<T> *curRoot = root;
while (curRoot) {
if (curRoot->data == data)
return curRoot;
if (data < curRoot->data) {
curRoot = curRoot->pLeft;
} else {
curRoot = curRoot->pRight;
}
}
return nullptr;
}二叉搜索树的结点删除
相比于插入和查找,二叉搜索树的删除显得复杂得多,我们应当如何在删除结点之后仍然保持二叉搜索树的性质不变呢?
其实删除也并不复杂,主要分为三种情况:
- 要删除的结点只有右子树而无左子树
- 要删除的结点只有左子树而无右子树
- 要删除的结点既有左子树也有右子树
首先看比较简单的前两种情况。
假设我们有这样一棵简单的二叉搜索树:

- 如果我们要删除的结点是
6也就是根结点,那么我们直接将二叉搜索树的根结点指向右结点即可。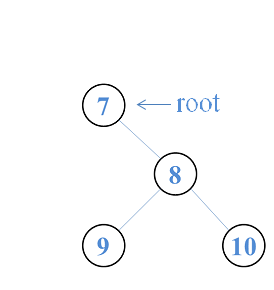
- 假设我们要删除的结点是
7,那么只需将7的父节点指向7的指针指向7的右结点即可。
- 如果要删除的结点是
9或者10,那么情况就相对简单,直接删除这个连接即可。
而对于只有左子树的结点而言,只是左右对调了而已,跟上面所说的没有什么不同,因此不再赘述了。
接下来看最复杂的第三种情况:
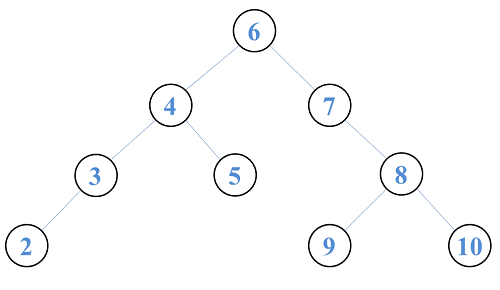
假如二叉树变成现在这样复杂的一棵,如果我们要删除结点 6,那么我们需要在左右子树中找到一个结点来维持二叉搜索树的性质。
容易想到,我们只需要用左子树中最大的结点,或者是右子树中最小的结点来替换我们的根结点即可。问题到这里就迎刃而解了,左子树中最大的结点,就是左子树中最右边的结点;同理,右子树中最小的结点,就是右子树中最左边的结点。我们只需要跟随着左右子树的右左指针不停向下遍历,直到遇到空指针即可。
而所谓的“替换”其实是将两个结点的值对调了,然后删除原来的结点而已。而很显然,要删除的这个结点只有一边有子树,或者是叶子结点,这就回归到了上面两种简单的情况上,是不是觉得其实这种复杂的情况很简单呢?
具体代码如下:
template<class T>
TreeNode<T> *BST<T>::remove(T data) {
TreeNode<T> *parent, *node;
parent = nullptr;
node = root;
while (node) {
if (node->data == data)
break;
parent = node;
if (data < node->data)
node = node->pLeft;
else
node = node->pRight;
}
if (node == nullptr) return nullptr;
// 1. 为叶子结点
if (node->pLeft == nullptr && node->pRight == nullptr) {
if (parent->pLeft == node) parent->pLeft = nullptr;
if (parent->pRight == node) parent->pRight = nullptr;
return node;
}
// 2. 只有左子树而无右子树
if (node->pLeft && node->pRight == nullptr) {
if (parent == nullptr) {
root = node->pLeft;
return node;
}
if (parent->pLeft == node) {
parent->pLeft = node->pLeft;
return node;
}
if (parent->pRight == node) {
parent->pRight = node->pLeft;
return node;
}
}
// 3. 只有右子树而无左子树,与上面的操作是对称的
if (node->pRight && node->pLeft == nullptr) {
if (parent == nullptr) {
root = node->pRight;
return node;
}
if (parent->pRight == node) {
parent->pRight = node->pRight;
return node;
}
if (parent->pLeft == node) {
parent->pLeft = node->pRight;
return node;
}
}
// 4. 左右子树都有
if (node->pLeft && node->pRight) {
TreeNode<T> *target;
// 这里我们可以随便选择左右子树
target = node->pLeft;
while (target->pRight) target = target->pRight;
this->remove(target->data);
node->data = target->data;
return target;
}
return nullptr;
}虽然删除的代码长了点,但是其实只是情况复杂了一点,并不困难,仔细分类就可以明白了。
总结
二叉搜索树是一种基础的数据结构,其三种操作的实现都并不太复杂,平均情况下可以提供 $O(\lg n)$ 的查找时间复杂度。
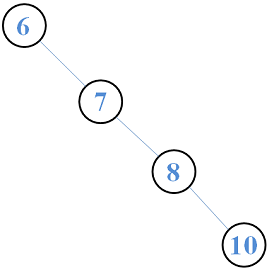
不过,如果遇到了这种情况,就是最坏的情况,这时候的查找复杂度退化为 $O(n)$。
如果我们能使二叉搜索树尽量保持平衡,那么就可以使得最坏情况下也有平均复杂度,这时候我们需要实现的数据结构便是平衡二叉搜索树,然而其实现比二叉搜索树更为复杂,详情另一篇博文更新再详细陈述。